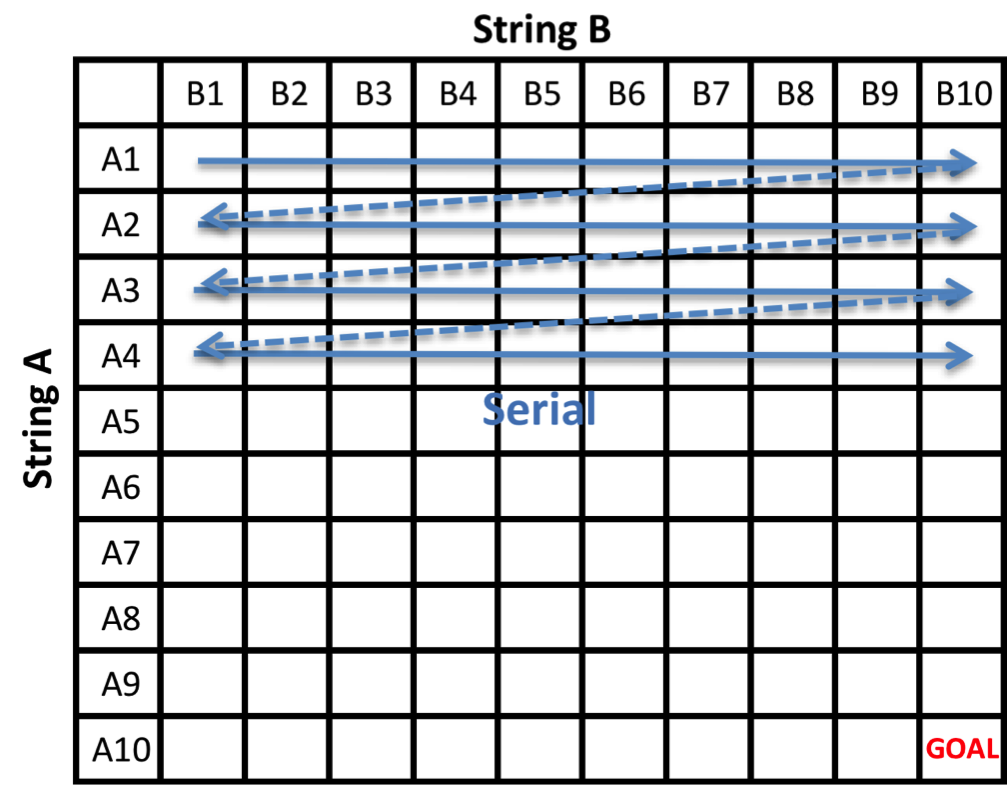
Serial Dynamic Programming

Data Dependency

The traditional bottom­-up dynamic programming algorithm is inherently difficult to parallelize due to the data dependence between overlapping subproblems. An alignment matrix is stored to keep intermediate values of edit distances between substrings of the two original string sequences. Each cell of the alignment matrix depends on the values in its left, upper, and upper left cells. The formula below illustrates this dependency, where x and y are the two strings being compared and D is the dynamic programming table.

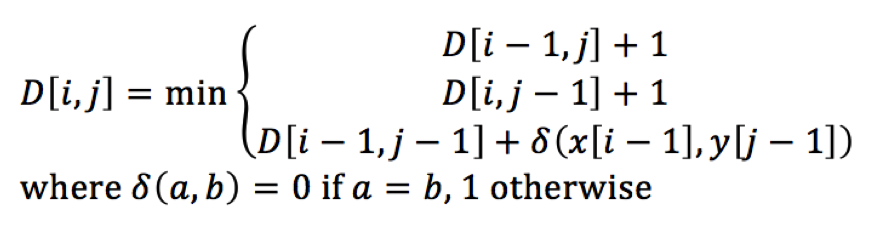
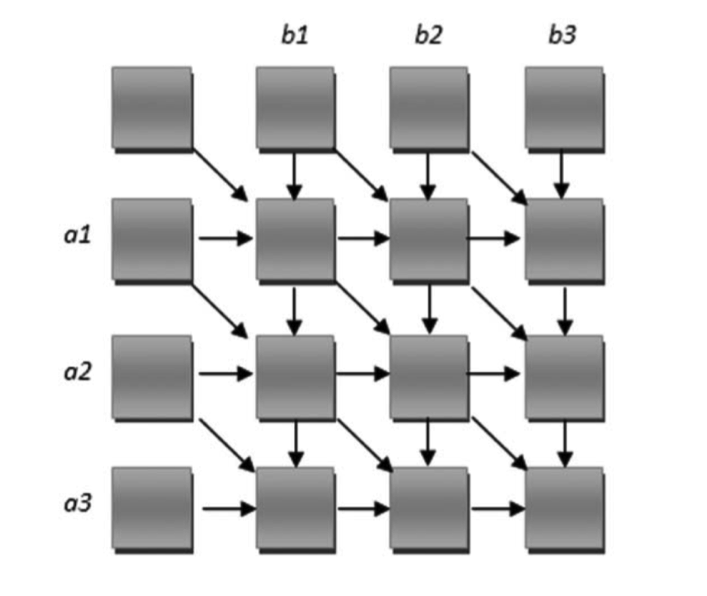
The following graph illustrates the dependency of the alignment matrix. This poses an interesting challenge for a parallel implementation.

Serial Algorithm

Our baseline serial approach is the standard dynamic programming algorithm for computing edit distances. We fill the alignment matrix row by row following the update formula given above. The bottom right cell gives the edit distance between the two string sequences.